pEqn.H File Reference

Include dependency graph for pEqn.H:

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Functions
volScalarField	rAU ("rAU", 1.0/UEqn.A())
surfaceScalarField	rhorAUf ("rhorAUf", fvc::interpolate(rho *rAU))
volVectorField	HbyA (constrainHbyA(rAU *UEqn.H(), U, p_rgh))
surfaceScalarField	phig (-rhorAUf *ghf *fvc::snGrad(rho) *mesh.magSf())
surfaceScalarField	phiHbyA ("phiHbyA",(fvc::flux(rho *HbyA)+rhorAUf *fvc::ddtCorr(rho, U, phi))+phig)
MRF	makeRelative (fvc::interpolate(rho), phiHbyA)
	constrainPressure (p_rgh, rho, U, phiHbyA, rhorAUf, MRF)
const volScalarField	psip0 (psi *p)
	for (int nonOrth=0;nonOrth<=nNonOrthCorr;nonOrth++)
thermo	correctRho (psi *p - psip0)
	if (thermo.dpdt())
	if (closedVolume &&compressible)

Variables
bool	closedVolume = p_rgh.needReference()
dimensionedScalar	compressibility = fvc::domainIntegrate(psi)
bool	compressible = (compressibility.value() > SMALL)
	rho = thermo.rho()
	p = p_rgh + rho*gh

Function Documentation

rAU()

volScalarField rAU	(	"rAU"	,
		1.0/UEqn.	A()
	)

rhorAUf()

surfaceScalarField rhorAUf	(	"rhorAUf"	,
		fvc::interpolate(rho *rAU)
	)

HbyA()

volVectorField HbyA

(

constrainHbyA(rAU *UEqn.H(), U, p_rgh)

)

phig()

surfaceScalarField phig

(

-rhorAUf *ghf *

fvc::snGradrho) *mesh.magSf(

)

phiHbyA()

surfaceScalarField phiHbyA	(	"phiHbyA"	,
		(fvc::flux(rho *HbyA)+rhorAUf *fvc::ddtCorr(rho, U, phi))+	phig
	)

makeRelative()

MRF makeRelative	(	fvc::interpolate(rho)	,
		phiHbyA
	)

constrainPressure()

constrainPressure	(	p_rgh	,
		rho	,
		U	,
		phiHbyA	,
		rhorAUf	,
		MRF
	)

psip0()

const volScalarField psip0

(

psi *

p

)

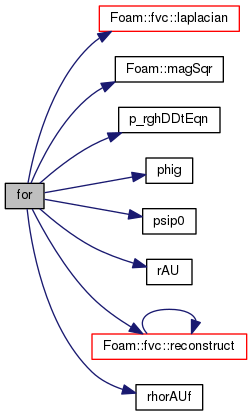
for()

for

(

int

nonOrth = 0; nonOrth<=nNonOrthCorr; nonOrth++

)

Definition at line 39 of file pEqn.H.

References fvOptions, Foam::fvc::laplacian(), Foam::magSqr(), mesh, nCorr, nNonOrthCorr, nOuterCorr, p, p_rgh, p_rghDDtEqn(), phi, phig(), phiHbyA, psi, psip0(), rAU(), Foam::fvc::reconstruct(), rhorAUf(), solvPerfp_rgh, thermo, and U.

Here is the call graph for this function:

correctRho()

thermo correctRho

(

psi *p -

psip0

)

if() [1/2]

if

(

thermo.

dpdt()

)

Definition at line 80 of file pEqn.H.

References Foam::fvc::ddt(), dpdt, and p.

Here is the call graph for this function:

if() [2/2]

if

(

closedVolume &&

compressible

)

Definition at line 93 of file pEqn.H.

References compressibility, Foam::fvc::domainIntegrate(), gh, initialMass, p, p_rgh, rho, and thermo.

Here is the call graph for this function:

Variable Documentation

closedVolume

bool closedVolume = p_rgh.needReference()

Definition at line 1 of file pEqn.H.

compressibility

dimensionedScalar compressibility = fvc::domainIntegrate(psi)

Definition at line 2 of file pEqn.H.

compressible

bool compressible = (compressibility.value() > SMALL)

Definition at line 3 of file pEqn.H.

rho

rho = thermo.rho()

Definition at line 5 of file pEqn.H.

p

p = p_rgh + rho*gh

Definition at line 77 of file pEqn.H.