alphaEqn.H File Reference

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Functions
word	alpharScheme ("div(phirb,alpha)")
tmp< fv::ddtScheme< scalar > >	ddtAlpha (fv::ddtScheme< scalar >::New(mesh, mesh.ddtScheme("ddt(alpha)")))
	if (isType< fv::EulerDdtScheme< scalar >>(ddtAlpha())||isType< fv::localEulerDdtScheme< scalar >>(ddtAlpha()))
else	if (isType< fv::CrankNicolsonDdtScheme< scalar >>(ddtAlpha()))
surfaceScalarField	phic (mixture.cAlpha()*mag(phi/mesh.magSf()))
	if (icAlpha > 0)
	forAll (phic.boundaryField(), patchi)
tmp< surfaceScalarField >	phiCN (phi)
	if (ocCoeff > 0)
	if (MULESCorr)
	for (int aCorr=0;aCorr< nAlphaCorr;aCorr++)
	if (alphaApplyPrevCorr &&MULESCorr)
	if (word(mesh.ddtScheme("ddt(rho,U)"))==fv::EulerDdtScheme< vector >::typeName)

Variables
scalar	ocCoeff = 0
	else
scalar	cnCoeff = 1.0/(1.0 + ocCoeff)
surfaceScalarField::Boundary &	phicBf

Function Documentation

word alpharScheme

(

"div(phirb,alpha)"

)

tmp<fv::ddtScheme<scalar> > ddtAlpha

(

fv::ddtScheme< scalar >

::Newmesh, mesh.ddtScheme("ddt(alpha)")

)

Referenced by if().

Here is the caller graph for this function:

if

(

isType< fv::EulerDdtScheme< scalar >>

ddtAlpha())||isType< fv::localEulerDdtScheme< scalar >>(ddtAlpha()

)

Definition at line 17 of file alphaEqn.H.

else if

(

isType< fv::CrankNicolsonDdtScheme< scalar >>

ddtAlpha()

)

Definition at line 24 of file alphaEqn.H.

References ddtAlpha(), Foam::exit(), Foam::FatalError, FatalErrorInFunction, nAlphaSubCycles(), and ocCoeff.

Here is the call graph for this function:

surfaceScalarField phic

(

mixture.

cAlpha)*mag(phi/mesh.magSf()

)

Referenced by for(), and if().

Here is the caller graph for this function:

if	(	icAlpha	,
		0
	)

Definition at line 51 of file alphaEqn.H.

References icAlpha(), Foam::MULES::interpolate(), Foam::mag(), mixture, phic(), and U.

Here is the call graph for this function:

forAll	(	phic.	boundaryField(),
		patchi
	)

Definition at line 62 of file alphaEqn.H.

References patchi, phi, and phiCN().

Here is the call graph for this function:

tmp<surfaceScalarField> phiCN

(

phi

)

Referenced by forAll().

Here is the caller graph for this function:

if	(	ocCoeff	,
		0
	)

Definition at line 75 of file alphaEqn.H.

References cnCoeff, and phi.

if

(

MULESCorr

)

Definition at line 80 of file alphaEqn.H.

References alpha1, alpha2, alphaApplyPrevCorr(), alphaPhi(), correct, Foam::endl(), Foam::Info, LTS, Foam::max(), mesh, Foam::min(), mixture, and talphaPhiCorr0.

Here is the call graph for this function:

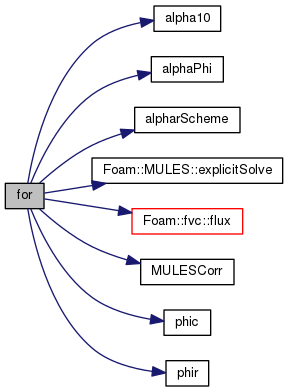
for

(

)

Definition at line 125 of file alphaEqn.H.

References alpha1, alpha10(), alpha2, alphaPhi(), alpharScheme(), cnCoeff, correct, Foam::MULES::explicitSolve(), Foam::fvc::flux(), mixture, MULESCorr(), phi, phic(), and phir().

Here is the call graph for this function:

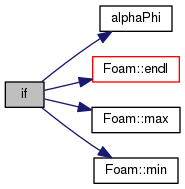
if

(

alphaApplyPrevCorr &&

MULESCorr

)

Definition at line 182 of file alphaEqn.H.

References alphaPhi(), and talphaPhiCorr0.

Here is the call graph for this function:

if

(

word(mesh.ddtScheme("ddt(rho,U)"))

= = fv::EulerDdtScheme<vector>::typeName

)

Definition at line 188 of file alphaEqn.H.

References alpha1, alphaPhi(), cnCoeff, Foam::endl(), Foam::Info, Foam::max(), mesh, Foam::min(), phi, rho1, rho2, and rhoPhi.

Here is the call graph for this function:

Variable Documentation

scalar ocCoeff = 0

Definition at line 15 of file alphaEqn.H.

Referenced by if().

else

Initial value:

{
        FatalErrorInFunction
            << "Only Euler and CrankNicolson ddt schemes are supported"
            << exit(FatalError)

Definition at line 39 of file alphaEqn.H.

scalar cnCoeff = 1.0/(1.0 + ocCoeff)

Definition at line 45 of file alphaEqn.H.

Referenced by for(), and if().

surfaceScalarField::Boundary& phicBf

Initial value:

=
        phic.boundaryFieldRef()

Definition at line 57 of file alphaEqn.H.