Base for a set of schemes which integrate simple ODEs which arise from semi-implcit rate expressions. More...
Public Member Functions | |
| TypeName ("integrationScheme") | |
| Runtime type information. More... | |
| declareRunTimeSelectionTable (autoPtr, integrationScheme, word,(),()) | |
| Declare runtime constructor selection table. More... | |
| integrationScheme () | |
| Construct. More... | |
| virtual autoPtr< integrationScheme > | clone () const =0 |
| Construct and return clone. More... | |
| virtual | ~integrationScheme () |
| Destructor. More... | |
| template<class Type > | |
| Type | delta (const Type &phi, const scalar dt, const Type &Alpha, const scalar Beta) const |
| Perform the integration. More... | |
| template<class Type > | |
| Type | partialDelta (const Type &phi, const scalar dt, const Type &Alpha, const scalar Beta, const Type &alphai, const scalar betai) const |
| Perform a part of the integration. More... | |
| virtual scalar | dtEff (const scalar dt, const scalar Beta) const =0 |
| Return the integration effective time step. More... | |
| virtual scalar | sumDtEff (const scalar dt, const scalar Beta) const =0 |
| Return the integral of the effective time step. More... | |
Static Public Member Functions | |
| static autoPtr< integrationScheme > | New (const word &phiName, const dictionary &dict) |
| Select an integration scheme. More... | |
| template<class Type > | |
| static Type | explicitDelta (const Type &phi, const scalar dtEff, const Type &Alpha, const scalar Beta) |
| Perform the integration explicitly. More... | |
Base for a set of schemes which integrate simple ODEs which arise from semi-implcit rate expressions.
![\[ \frac{d \phi}{d t} = A - B \phi \]](form_183.png)
The methods are defined in terms of the effective time-step 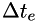 by which the explicit rate is multiplied. The effective time-step is a function of the actual time step and the implicit coefficient, which must be implemented in each derived scheme.
by which the explicit rate is multiplied. The effective time-step is a function of the actual time step and the implicit coefficient, which must be implemented in each derived scheme.
![\[ \Delta t_e = f(\Delta t, B) \]](form_185.png)
![\[ \Delta \phi = (A - B \phi^n) \Delta t_e \]](form_186.png)
This class also facilitates integration in stages. If the explicit and implicit coefficients, 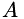 and
and 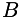 , are a summation of differing contributions,
, are a summation of differing contributions, 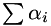 and
and 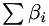 , then the integration can be split up to determine the effect of each contribution.
, then the integration can be split up to determine the effect of each contribution.
![\[ \frac{d \phi_i}{d t} = \alpha_i - \beta_i \phi \]](form_191.png)
![\[ \Delta \phi_i = \alpha_i \Delta t - \beta_i \int_0^{\Delta t} \phi d t \]](form_192.png)
![\[ \Delta \phi_i = (\alpha_i - \beta_i \phi^n) \Delta t - \beta_i (A - B \phi^n) \int_0^{\Delta t} t_e dt \]](form_193.png)
These partial calculations are defined in terms of the integral of the effective time-step, 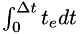 , which is also implemented in every derivation.
, which is also implemented in every derivation.
Definition at line 88 of file integrationScheme.H.
Construct.
Definition at line 38 of file integrationScheme.C.
|
virtual |
Destructor.
Definition at line 44 of file integrationScheme.C.
| TypeName | ( | "integrationScheme" | ) |
Runtime type information.
| declareRunTimeSelectionTable | ( | autoPtr | , |
| integrationScheme | , | ||
| word | , | ||
| () | , | ||
| () | |||
| ) |
Declare runtime constructor selection table.
|
pure virtual |
Construct and return clone.
Implemented in analytical, and Euler.
|
static |
Select an integration scheme.
Definition at line 32 of file integrationSchemeNew.C.
References Foam::endl(), Foam::exit(), Foam::FatalError, FatalErrorInFunction, Foam::Info, dictionary::lookup(), and Foam::nl.
|
inlinestatic |
Perform the integration explicitly.
Definition at line 32 of file integrationSchemeTemplates.C.
References integrationScheme::delta().

|
inline |
Perform the integration.
Definition at line 45 of file integrationSchemeTemplates.C.
References integrationScheme::partialDelta().
Referenced by integrationScheme::explicitDelta().


|
inline |
Perform a part of the integration.
Definition at line 58 of file integrationSchemeTemplates.C.
Referenced by integrationScheme::delta().

|
pure virtual |
Return the integration effective time step.
Implemented in analytical, and Euler.
|
pure virtual |
Return the integral of the effective time step.
Implemented in Euler, and analytical.